Confidential Data in the Cloud

Cloud computing has caused a major change in the IT world. Securely processing private or sensitive data in the cloud is not always possible, and sometimes it’s even against the rules (for example, business, medical, or banking data). Encrypting data is only part of the solution because you still need to decrypt it to use it.

Managing the secrets involved is often very difficult from a security standpoint:

• you can hard-code them in software;
• you can rely on hardware capabilities to secure them (confidential computing);
• or you can use software protection techniques.

It’s not a good idea to put secrets directly into source code. An experienced reverse engineer will find them in minutes. These secrets are also in clear in RAM. In certain cases, you can ask the user for a password, but it’s usually low-entropy secrets. This issue can be somewhat addressed if it is possible to interact with a backend (involving a Password-Authenticated Key Agreement protocol), but this does not solve the clear-data-in-RAM issue!

Often, there is no secret that can be trusted to implement: code authenticating itself to a backend; data decryption on local storage; subcontracting computations to an untrusted actor (cloud provider).

Confidential computing is implemented using technologies such as Intel SGX, ARM TrustZone, Apple Secure Enclave, etc. However, these trust models may not always meet your security needs. Customers of traditional cloud providers (Google, Amazon, Azure, etc.) have little choice but to trust them and trust the CPU makers Intel/AMD.

The Apple model is better adapted because the customer (Apple software) and the cloud provider (a mobile phone running iOS on Apple hardware) are the same. In this case, Apple only needs to trust itself.

Software protection techniques, such as code obfuscation and tamper-proofing have a limited security: they allow to slow down an adversary, but not to stop them. White-box cryptography is slightly more robust, but still does not provide any cryptographic-level guarantees and the set of available cryptographic operations is restricted.

The following picture provides a summary about these technologies.

Advanced Cryptography

What about advanced cryptography techniques to ensure the confidentiality of secret data? Here is the idea: keep your secrets in a safe place. Use encryption to protect the data. Then, process the encrypted data in an environment you don’t trust. In other words: compute on encrypted data!

Computing on encrypted data has been an active research area since the 1980’s. Several protocols have been implemented and put into production by some companies in the recent past.

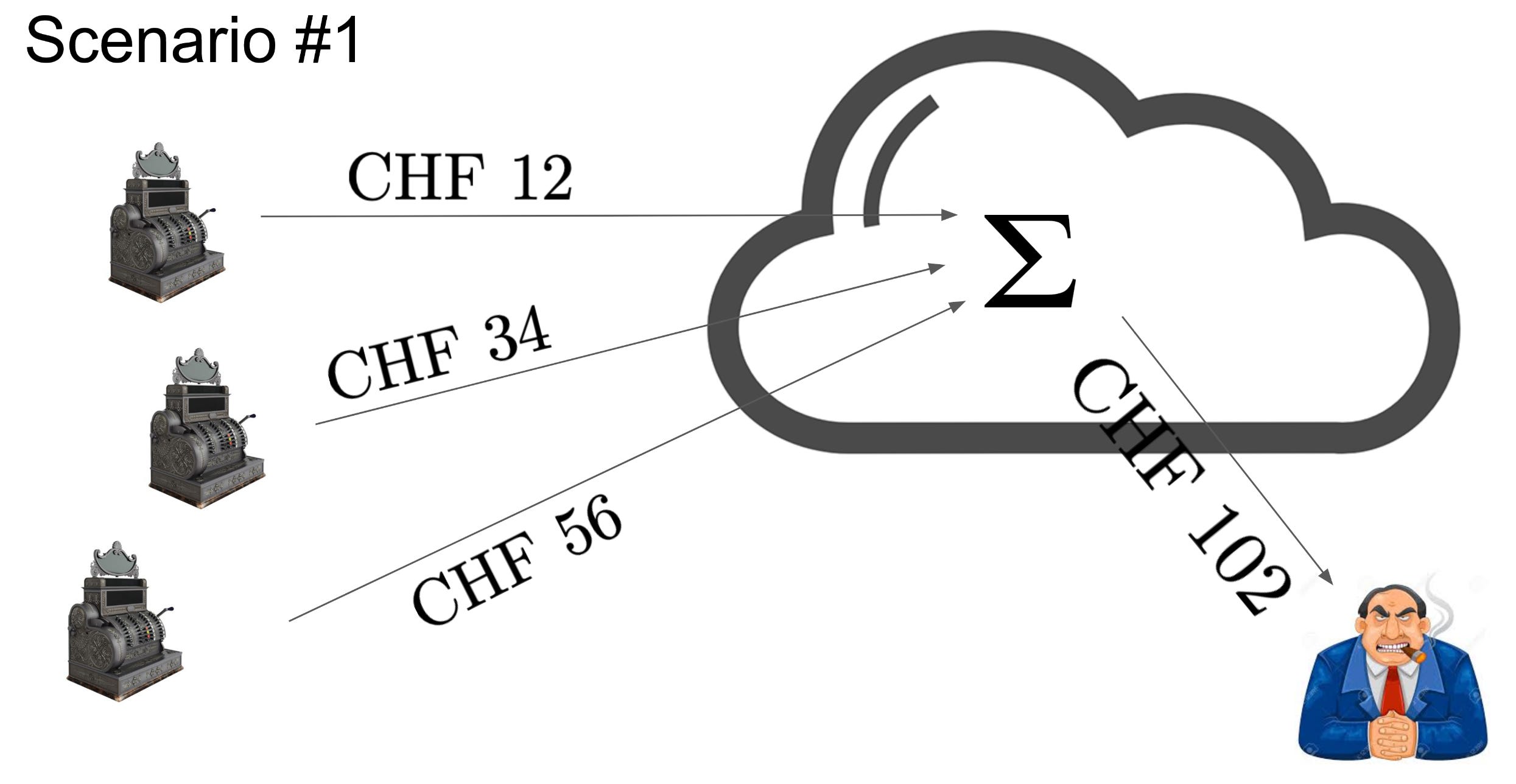
Here is a motivating scenario: you want to calculate the total sales of several subsidiaries in the cloud. Of course, these figures are confidential. In the first scenario, there is no encryption at work. This means that an adversary can break the confidentiality of this data either while it is in transit from a subsidiary to the cloud, while it is being processed in the cloud, or while it is in transit from the cloud to headquarters.

A second scenario involves the protection of the confidential data in transit, by relying on the TLS 1.3 protocol, for example.

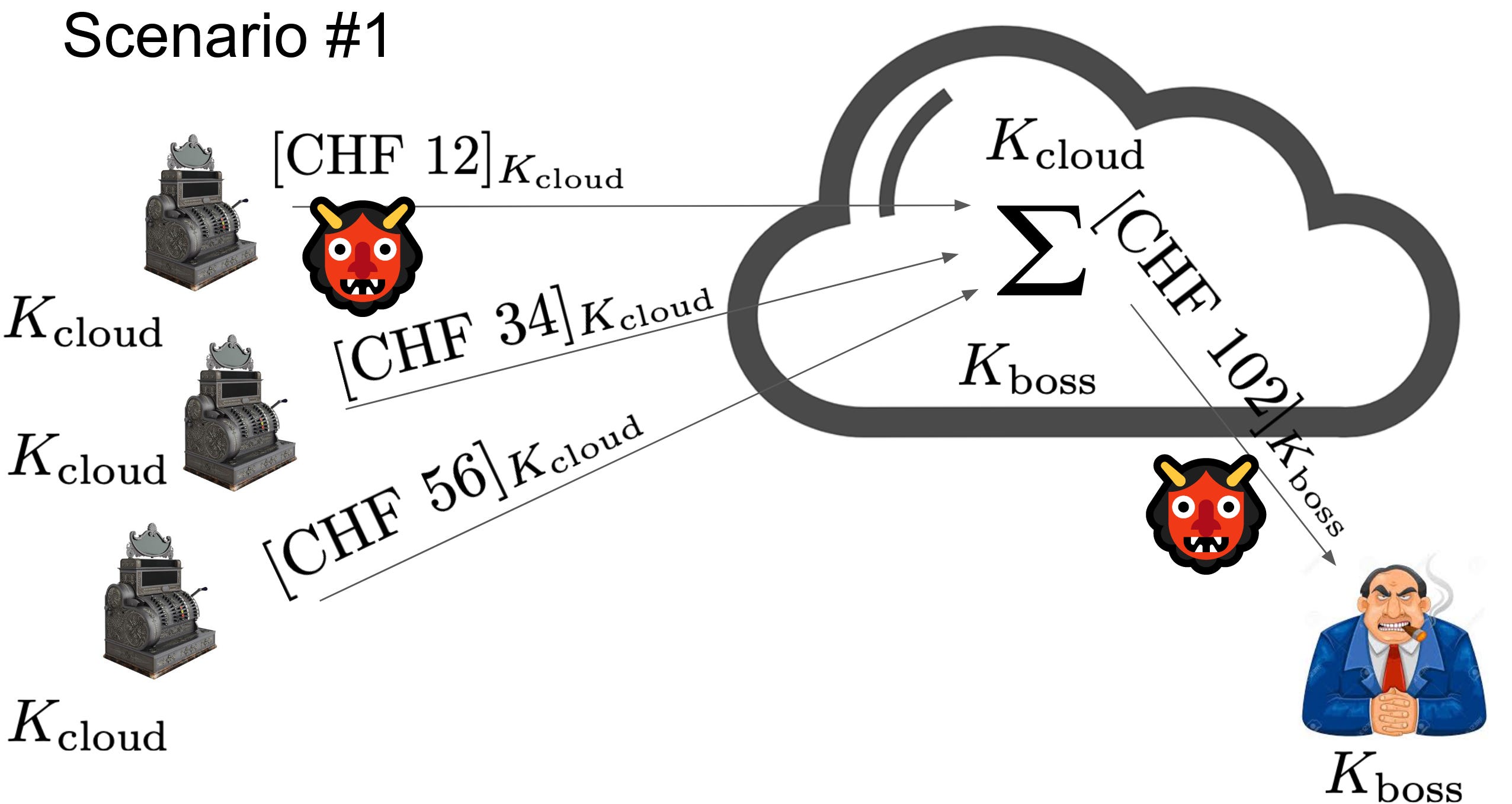
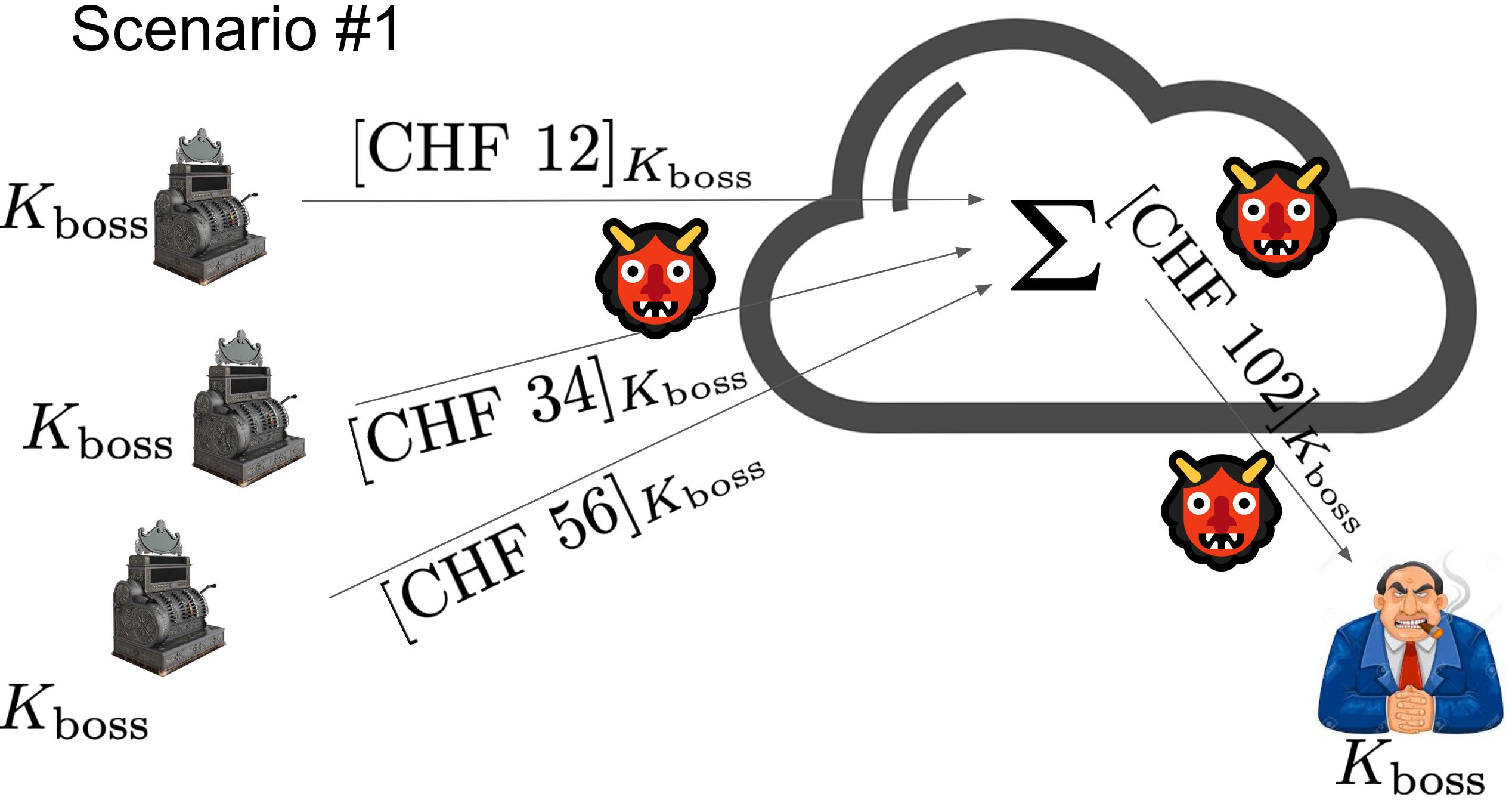
In this scenario, an adversary cannot access the confidential data while it is in transit. However, the data is decrypted, processed, and then re-encrypted in the cloud, which means it can be stolen here.

Homomorphic encryption allows you to encrypt data, compute its sum without decrypting it in the cloud, and then decrypt it in a trusted location. In this scenario, data confidentiality is guaranteed everywhere.

The useful mathematical properties of homomorphic encryption are the following:

Homomorphic encryption forms the core of several secure protocols, such as E-cash, E-voting, threshold cryptography, etc.

Another motivating example is the following: Alice's portfolio contains various stocks and she wants to compute the associated risk. She has implemented an algorithm based on logistic regression to compute this value. Alice would like to outsource the risk computation to a cloud provider without revealing her portfolio structure or the coefficients of her logistic regression model.

Alice’s portfolio is modeled as $x_1, x_2, …, x_n$ and her logistic regression model can be represented by its coefficients $\alpha_1, \alpha_2, …, \alpha_n$. The function to be calculated is $x_1\cdot\alpha_1 + ... + x_n\cdot\alpha_n$.

Using an homomorphic encryption scheme does not work anymore, as one can either add OR multiply ciphertexts, but not both at the same time ! One needs new cryptographic magic, named a Fully Homomorphic Encryption (FHE) scheme.

Fully Homomorphic Encryption

In 2009, Craig Gentry achieved a theoretical breakthrough with fully homomorphic encryption (FHE). Homomorphic operations can be either XOR and AND, or addition and multiplication in a ring.

Here is a typical API of such schemes:

• KeyGen(): takes a security parameter in input and returns apublic key, a decryption key and a (public) evaluation key.
• Encrypt(): takes the public key and a plaintext, and returns aciphertext.
• Eval(): takes the evaluation key, one or more ciphertextsand/or evaluation results, and returns a ciphertext.
• Decrypt(): takes a ciphertext or an evaluation result and thedecryption key, and it returns a plaintext.

There are several variants of fully homomorphic encryption schemes: somewhat homomorphic encryption schemes do not necessarily support all types of circuits. The size of their ciphertext may increase with each homomorphic operation. Leveled homomorphic encryption schemes support all circuits of depth at most d. Their ciphertext’ size does not depend on d. Finally, fully homomorphic encryption schemes support all circuits and the ciphertext size does not depend on the circuit depth d.

Several startups are currently active in the field, especially in the area of privacy-preserving machine learning.

Secure Multi-Party Computation

Different parties $P_1, …, P_n$ have each a secret input xi, and they do not trust each other. They would like to compute together a known function

without disclosing any information about their secret inputs. Security must be kept even if some parties collude together, or are compromised by the same adversary.

One possibility would be to rely on a third party that is trusted by all parties: each of them gives its input to the trusted third party, which evaluates the function and sends the result to all parties.

When no trusted third party is available, one can run a secure multi-party computation protocol (MPC).

There are different security models that address these protocols: adversaries can be semi-honest, or passive, which means they execute the protocol as expected, but try to gather information about the other participants' inputs. Malicious, or active adversaries try to gather information by actively corrupting other parties or deviating from the protocol. Secure multi-party computation protocol might tolerate a variable amount of corrupted parties. Finally, their security might depend on the various types of guarantees offered by the network

Yao Garbled Circuits

One of the oldest secure multi-party computation protocol are garbled circuits. Alice and Bob would like to compute a secure “comparator” on secret inputs.

The protocol stages are as follows:

• First, Alice and Bob define the function to be evaluated as a Boolean circuit with 2-input gates.
• Second, Alice “garbles” the circuit, i.e, “encrypts” it and sends it to Bob, together with her encrypted inputs.
• Bob receives his own encrypted inputs from Alice through oblivious transfer (see below).
• Bob evaluates the circuit and gets the encrypted output.
• Alice and Bob collaborate to decrypt the output.

It’s a secure protocol for semi-honest adversaries. The protocol is efficient, since the number of communication rounds is independent of the Boolean circuit size.

Oblivious transfer is an important MPC protocol brick. It works as follows: Alice has two strings $m_0$ and $m_1$ and Bob generates a random bit $i$. Alice sends $m_i$ in such a manner that she learns nothing about $i$ and Bob learns nothing about $m_{1-i}$.

Private Set Intersection

Sometimes protocols for specific settings are much more efficient than MPC protocols allowing to evaluate any circuit. Here is an example: Alice possesses a database with items

Bob possesses a database with items

Alice would like to compute the intersection of $X$ and $Y$ such that she does not learn any information outside the intersection of $X$ and $Y$ and Bob learns nothing about $X$. Protocols of private set intersection (PSI) allow to securely compute the intersection of two sets containing confidential data. Its use cases are pattern matching (testing human genomes), privacy-preserving intersection of lists of contacts, suspects, or compromised credentials, and computing private join-and-compute operations in the realm of online advertising.

While not yet a silver bullet, solutions based on advanced cryptography will play an important role in securing sensitive data in the cloud.

In the next episode, I’ll cover remote attestation. Stay tuned!

Thanks for reading Crumbs of Cybersecurity! Subscribe for free to receive new posts and support my work.